Fish-eye cameras are used in applications where the field of view to be observed is larger than what can be observed with wide-angle (rectilinear) lenses. The maximum theoretical field of view of a rectilinear camera is less than 180 degrees, but in practice, ultra-wide lenses tend to have fields of view (FOV) going up to around 120 degrees to avoid excessive distortions, whereas fish-eye lenses can cover up to 180 degrees or more. Typical applications for fish-eye lenses, to name just a few, include vehicle surround view and in-cabin monitoring systems, as well as CCTV cameras. It is important to note that unlike in the case of rectilinear lenses, there are many different types of fish-eye lenses, each with its own projective function.
At AILiveSim, in our simulator, we have implemented several different types of sensors, such as RGB and IR (operating at different wave length) cameras, LIDARs, and RADARs. To ensure our sensors closely match those used by our clients, we have integrated a range of lenses featuring various distortion types for the cameras. This alignment is critical, particularly when training or testing, a deep-learning computer vision solution with simulated data, to circumvent the so called “out-of-distribution” problem. Essentially, for an algorithm to perform optimally when deployed in a system, it’s imperative that the simulated sensor closely mimics the physical one. For instance, if the target system employs a fish-eye lens with an equidistant projection function, training and testing the algorithm with images from a camera that simulates this specific function would be beneficial.
In the realm of deep learning, “out-of-distribution” can signify various discrepancies, but in this context, it refers specifically to the nature of the signal processed by the algorithm. If an algorithm is trained on data from a certain distribution and later applied to a system where the data originates from a markedly different distribution, the algorithm’s performance can significantly deteriorate.
Projective Functions
In this article I will explain how two distinct types of fish-eye lenses, namely the equidistant and the equisolid angle lenses, can be modeled mathematically using a spherical projection model.
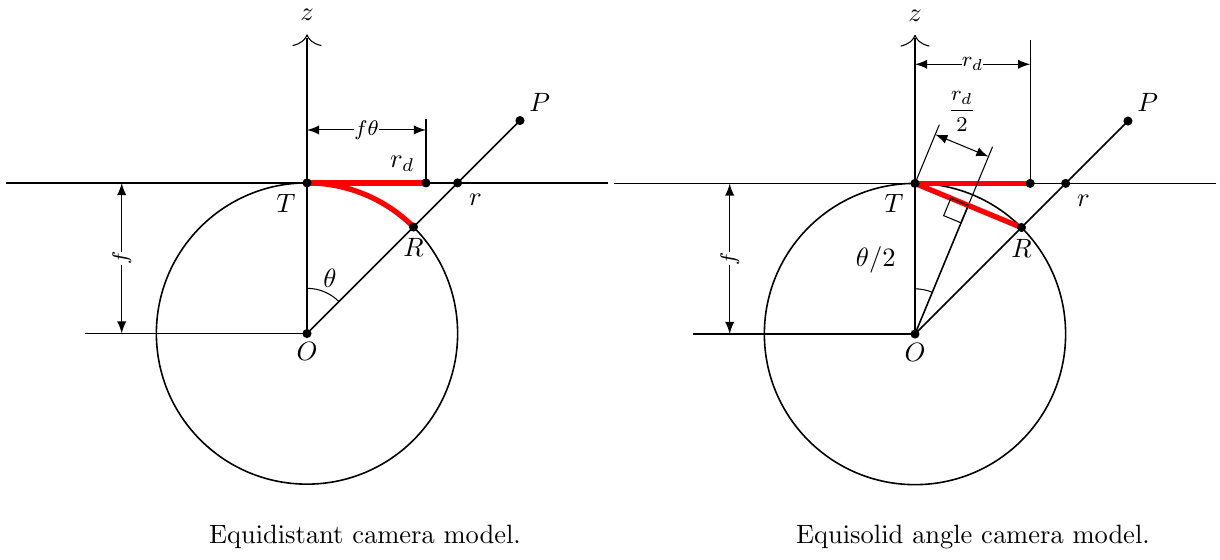
Consider a point P in 3D space being projected onto the camera. Here, f represents the focal length, r denotes the projection of P onto a rectilinear camera, and rd represents the projection of P onto the equidistant or equisolid angle cameras. Theta is the incident angle between the incoming ray and the optical axis.
For the equidistant lens, the distance rd from the optical center is equivalent to the arc length TR, defined by f*theta. Conversely, for the equisolid angle lens, the distance of rd from the optical center is directly related to the length TR. Through a bit of algebra, we find that for the equidistant lens, we have rd=f*theta, and for the equisolid angle lens, we have rd=2*f*sin(theta/2).
These projection functions reveal that the farther we move from the optical axis, the more these functions compress the image. Additionally, it’s noteworthy that the maximum theoretical field of view for a rectilinear camera is less than 180 degrees.
Use Cases
Since the projective functions are different, equidistant and equisolid angle lenses are used in slightly different applications:
- Equidistant lens: Equidistant lenses are particularly valued in applications that require accurate angular measurements across the image, such as in sky surveys, astronomy, and panoramic photography. They are also used in mapping and surveying applications where accurate distance representation is crucial.
- Equisolid angle lens: Equisolid angle lenses are often used in applications where maintaining the relative area is important, such as in certain scientific and meteorological observations, where accurate measurement of cloud coverage or star fields is needed.
Equidistant Lens in Action
In the following image, we observe the effect of an equidistant lens. The top image depicts how a scene would appear when captured by a rectilinear camera with a field of view (FOV) of 150 degrees, while the bottom image shows the same scene captured with an equidistant lens. With the equidistant lens, as we approach the edges of the image, information becomes increasingly compressed, resulting in the bending of straight lines.

Thank you for reading. I hope this article provided valuable insights into projective functions of fish-eye lenses. Please feel free to share your thoughts or questions in the comments below.
